Tricubic Cartesian Canine Example

Description

• This example guides you through setting up and running a physical and material nonlinear problem of the contraction of a dog heart in the circulation.
• The mesh of the left and right ventricle was fitted to a dog heart. The basis functions for the mesh coordinates are cubic in all directions (cubic-cubic-cubic) and tri-linear for the fiber architecture. The passive material chosen is a transversely isotropic exponential strain energy function. Pressure is prescribed on the LV and RV endocardium, and is computed by a lumped-parameter systems model of the closed circulation. Active stress is calculated by a varying-elastance type cellular model (Guccione model) and is added to the passive stress in the fiber direction. A fraction of the active stress is also added to the passive stress perpendicular to the fibers. Active stress is dependent on time, sarcomere length (which is proportional to fiber strain), and calcium concentration.

Start Continuity

• Launch the Continuity 6.3 Client

• On the About Continuity 6.3 startup screen

  • Leave the mesh checkbox checked under Use Modules:

  • In addition, check the biomechanics checkbox

• Click OK to bring up the main window

Create mesh

• File→Load→Model…

  • Select the cont6 file for this tutorial (dog_rva_pacing_circmodel.cont6)

  • To make sure you selected the right cont6 file, verify the following:

    • Mesh→Edit→Basis…

      • Check that the list contains only:
        • Cubic-Cubic-Cubic Hermite 3*3*3
        • Cubic-Cubic Hermite 3*3
        • Linear-Linear-Linear Lagrange 3*3*3
        • Linear-Linear Lagrange 3*3

    • Mesh→Edit→Nodes…

      • Check that that there are only 82 nodes defined

        (dog_rva_pacing_circmodel_nodes.txt)

    • Mesh→Edit→Elements…

      • Check that there are 5 pages of 48 elements in the list

        (dog_rva_pacing_circmodel_elements.txt)

    • Mesh→Edit→Material Coordinates …

      • Click on the Submit tab and click on Submit button

• File→Send

  • If the Dimensions Form appears, simply click Apply Marked Recommendations and then OK

• Mesh→Calculate Mesh…

• Mesh→Render→Elements…

  • Click the lines radio button

  • Ensure the undeformed radio button is selected

  • Click Render to display mesh lines

• Mesh→Render→Elements…

  • Click the lines radio button

  • This time select the deformed radio button is selected

  • Click Render to display mesh lines

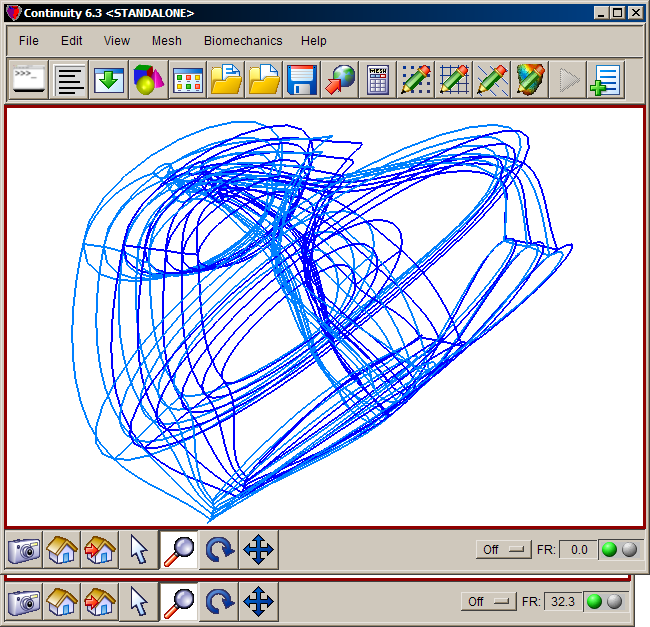
• The mesh should now look similar to the first screen shot

• Biomechanics→Edit→Constitutive Model

  • Select TI_of_Lagrangian_strains_comp_sympy: Traversely isotropic exponential function of Lagrangian strains, slightly compressible (sympy)

  • Click on Submit tab and click on Submit

• Biomechanics→Edit→Active stress… (simply click OK)

• Biomechanics→Edit→Circulation model… (simply click OK and OK)

Solve biomechanics

• If the Biomechanics menu is not loaded, select File→Load Continuity Modules…

  • Select biomechanics and click OK

  • The menu bar should now show the Biomechanics command

• Biomechanics→Solve Nonlinear…

  • For Time Step, enter 4.0

  • For Number of Steps, choose 1

  • For when number of iterations >, enter 150

  • For when sum of solution increments <, enter 1e-005

  • For when sum of unconstrained residuals <, enter 1e-005

  • Click Solve, and wait for the solver to finish

• Biomechanics→Render→Strain…

  • Select the deformed radio button on the bottom

  • Click Render

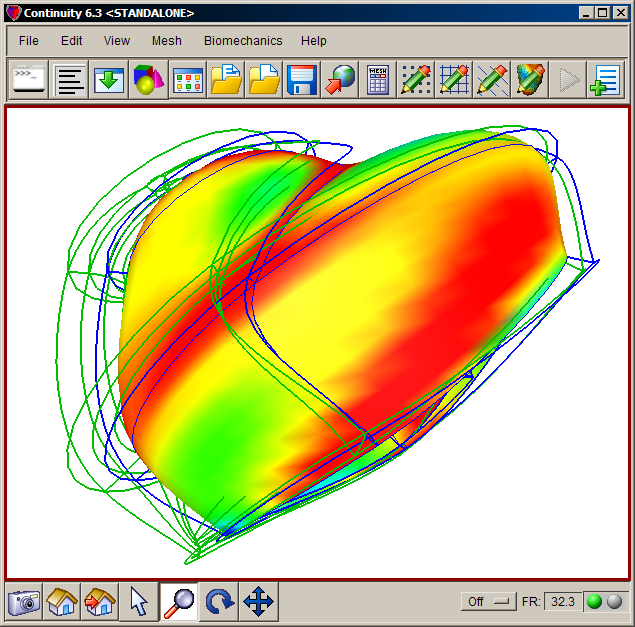
• The mesh should now look similar to the last two screenshots, viewed from different angles.

Pre-built model

This cont6 file you used above for this problem already contains all data and parameters, right up to the biomechanics solve.